昨天講到了梯度下降法則，今天要跟大家介紹的是反向傳播，它們兩個在神經網路中各自承擔著不同的任務。介紹完反向傳播後會帶入學習率的概念給的大家。

梯度下降法主要是計算損失函數的梯度（斜率），然後沿著梯度的方向更新參數以減少損失。他會用到數學的「微分」概念去找到極值。如果今天只面對一層神經網路當然綽綽有餘，可是我們面對的往往不止一層，而是很多層的神經網路，為了更有效率地找出梯度，是時候派上我們的「反向傳播」出場了！

反向傳播

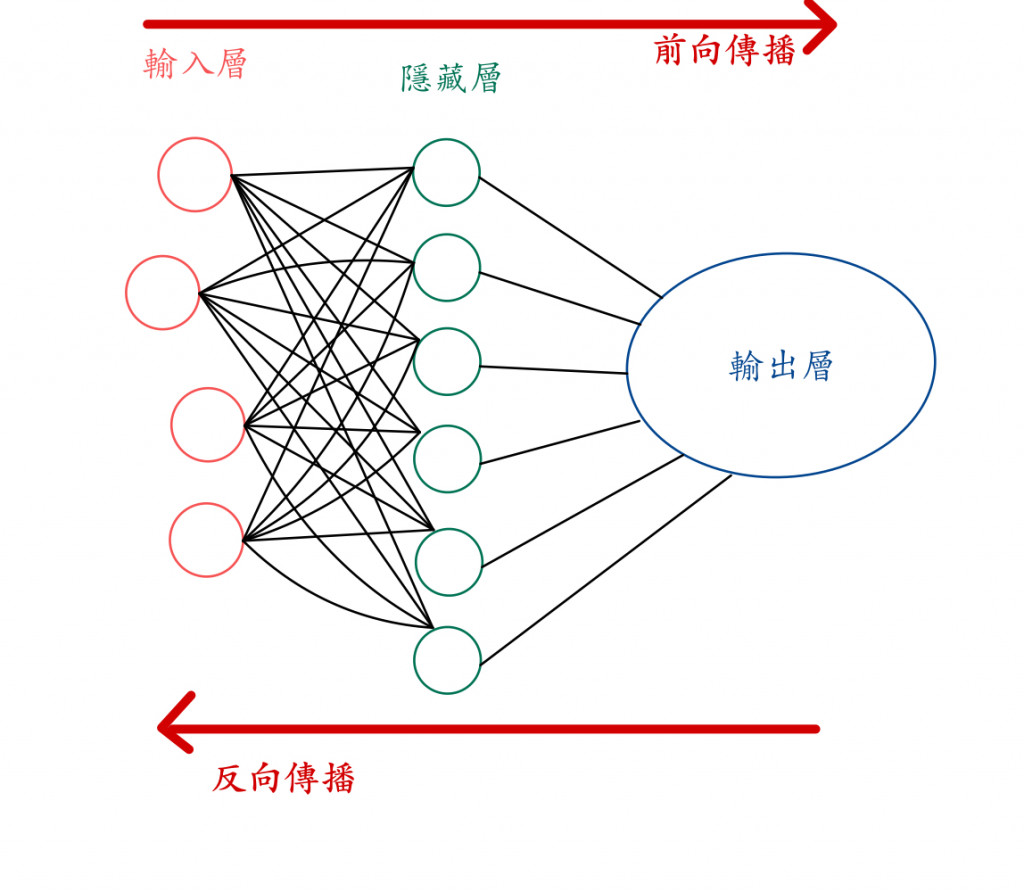
反向傳播是一種用於計算梯度的技術，利用微積分的連鎖法則（chain rule）來計算梯度，它將每一層的梯度傳回前一層，直到計算出所有參數的梯度。不知道大家還記不記得前向傳播（神經網路一層一層地往下計算），反向傳播就是相反從輸出端的權重梯度計算回輸入端。

學習率

我們做了那麼多的事情，總是要有東西告訴網路神經每次訓練的調整幅度，而這個就會跟學習率（Learning Rate）有關。學習率的選擇對訓練神經網路的效能和速度有著重要的影響。

• 學習率的作用：

  • 學習率控制了參數更新的大小。如果學習率過小，模型的訓練速度會變得非常緩慢，需要修正很多次才能找到損失最低點。另一方面，如果學習率過大，模型參數的更新幅度會太大，可能會使訓練過程不穩定，來回在低點附近跳動，始終找不到最低點。

• 學習率的選擇：

  • 學習率通常需要手動調整，一般的做法是從0.1或0.01開始，然後逐漸調整觀察模型的表現。常見的學習率包括0.1、0.01、0.001等。通常情況下，較大的學習率適用於具有大量訓練資料的模型，而較小的學習率適用於資料較少的模型。

看看我們之前寫過的程式，是不是更有感呢？loss='mean_squared_error'跟learning_rate=0.01相信大家都比當初還要更了解了！

model.compile(loss='mean_squared_error',optimizer=optimizers.SGD(learning_rate=0.01),metrics=['accuracy'])

今日總複習： 梯度下降法和反向傳播是相互依賴的。反向傳播透過有效地傳遞梯度訊息，幫助梯度下降法找到合適的參數值以最小化損失函數。